Research Article - Onkologia i Radioterapia ( 2020) Volume 14, Issue 4
Inspection of the global behaviour of a radiogenic cancer treatment nonlinear model
Kaushik Dehingia1*, Bhagya Jyoti Nath2, Hemanta Kumar Sarmah1 and Anusmita Das12Department of Mathematics, Barnagar College, Sorbhog, Assam, India
Kaushik Dehingia, Department of Mathematics, Guwahati University, Assam, India, Email: kaushikdehingia17@gmail.com
Received: 03-Jul-2020 Accepted: 20-Jul-2020 Published: 30-Jul-2020
Abstract
Neoplastic diseases are liable for 12% of deaths around the world. The researchers of several disciplines tried to observe the dynamics of tumour growth with the response to other cell population of the physical body. They need the used ever-new technique to regulate the tumour growth and its eradication from the physical body. Clinically, there are many treatment strategies like surgery, chemotherapy, radiotherapy, gene therapy, immunotherapy and combination of this etc. to beat the disease. During this paper, we analysed a model for the effect of radiogenic therapy within the treatment of cancer. Local stability analysis at various equilibrium points has discussed during this paper. For greater interest, we have shown that the tumour free equilibrium point is globally asymptotically stable. We even have done numerical verification of our mathematical result.
Keywords
Cancer, radiogenic therapy, positivity, bounded-ness, local stability, global stability
Introduction
A multi-faceted disease, which involves heterogeneous interaction between abnormal cells and surrounding environment of it, called Cancer [1]. When the body is not capable to control the growth of abnormal cell and when the body cell lose their ability to die, occur cancer [2]. Surgery, chemotherapy, radiotherapy, hormone therapy, and immunotherapy, either in isolation or in the combination of two or more of these are prominently used in cancer treatment [3]. With the utilization of radioisotopes, radiation is highly effective to eradicate tumours [4]. Chemotherapy is the treatment in which mostly used chemically designed drugs. Today, the researchers heavily busy with immunotherapy because it contains lesser side effects than other treatments. Immunotherapy increasing the effectiveness of the immune system to counter cancer cells by emphasizing the body's own natural ability to battle cancer. It encompasses the use of cytokines with ACI, engineering genetic antibody called (mAbs), and IL-2 therapy to improve or restore immune system function. However, chemo-immunotherapy enriches tumour recession and antitumor immune response [1]. Speciously vaccines, monoclonal antibodies, lymphocytes and cytokines are the key tools for tumour immunology [5]. The harshness of disease, treatment procedure and asset of patients’ immune system are the key factors on which cancer treatment depends [6-9].
Gene therapy may use when no other therapies which are mentioned above treated well to the patient’s body. By introducing a well-designed gene into the cells of a patient gene therapy correct an inborn inaccuracy of metabolism, alter or repair an acquired genetic abnormality, and provide a new function to a cell [10]. Recently, the research has proven that with the lesser effect on normal tissues a combination of gene and radiotherapy called radiogenic therapy may perform well in cancer curability [4,11,12]. Also, it has clinically demonstrated that the use of radiogenic therapy has many potential reimbursements with different toxicity profiles of both two therapies [13]. Radiations counter abnormal cells and increase the proliferation rate of the body’s immune cells and greater the anti-tumour response [11]. At the same time, gene therapy also kills tumour cells by inserting toxin genes under the control of a tumour-specific promoter and blocks the mechanisms by which tumours evade immunological destruction [2].
Mathematical modelling is increasing rapidly to predict the effectiveness of specific treatment. Modelling of any biological phenomena links the experimental result to computational results [14,15]. Mathematical models played an active role in the research of disease dynamics and are becoming instrumental in planning treatment strategies and give deep insight into understanding complex biological processes [16]. Modelling of cancer is usually divided into two phases, the one is to deal with the concept of the system without treatment, and another one is treatments in the evocative form [1]. Treatments with new features are evolved in nowadays, and it becomes a broad research area for any kind of researchers. In this study, we have proposed a radiogenic therapy cancer model by modifying the Tsygvintsev et al. gene therapy model [12] and based on radiotherapy model [9] with some assumptions. Further, we have analysed the dynamics of the model using the basics of mathematics.
Some mathematical preliminaries
Suppose that y=f(y) is a vector form of a set of nonlinear ODE. Suppose that y* is an equilibrium point. Let the Jacobian matrix corresponding to the equilibrium point y* be as J*.
Lemma: An equilibrium point y*of the differential equation y=f(y) is stable if all the eigenvalues of J*, the Jacobian evaluated at y*, have negative real parts. The equilibrium point is unstable if at least one of the eigenvalues has a positive real part [17].
Definition: A Lyapunov function W(Y) is a function consisting of state variables which has a minimum at an equilibrium point and which has no local minima [17].
Lemma: Let Ω be a region of phase space containing the equilibrium point y*. Let W: Ω→R be a continuous and differentiable function. W is a positive definite function for the point y* if it satisfies the following two conditions.
(i)W(y*) = 0 and
(ii) W(y)>0 for y∈Ω −{y*} [17]
Lemma: Let y* be an equilibrium point of the differential equation y=f(y) and let W be a positive definite function for this point. The equilibrium point is globally asymptotically stable i.e., the solutions tend to this point for initial conditions in the neighbourhood of y* if W (y) <0 for all y ∈ Ω -{y*} [17].
The model
In this study, we formulate our model that primarily based on Tsygvintsev et al. [12] gene therapy model. The model deals with effector cell population E(t), tumour or cancerous cell population T(t), gene therapy u1 (one kind immunotherapy) and a single dose of radiotherapy γ.
The effector cell: To model effector cells E(t) at any time
t>0, our first assumption is that the NK cells, Interleukin-2,
LAK, Lymphocytes, T helper cells all belong to effector cells
population. Next, we supposed that during gene therapy, the
immune system strongly respond to the tumour site and it is
represented by the term cT. The effector cells proliferate itself
in its site which is represented by a Michaelis-Menten fashion 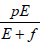 , which is a decreasing function of effector cells. –dE is
the natural decay of effector cells. The external immunotherapy
source to the effector site is represented by the term u1, which
is time-dependent. From these assumptions, the dynamics
of effector cell population can be expressed by the differential
equation
, which is a decreasing function of effector cells. –dE is
the natural decay of effector cells. The external immunotherapy
source to the effector site is represented by the term u1, which
is time-dependent. From these assumptions, the dynamics
of effector cell population can be expressed by the differential
equation
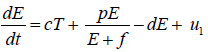
The tumour cell: Tumour cells T(t) proliferate logistically which
can be modelled by rT(1-bT), at any time t>0 with parameters
and b assigning the cancer growth rate and cancer cell capacity
respectively. The term 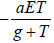 used for the high cancer clearance
during gene therapy with the effector cells negative response.
The single-dose radiation γ kills only the tumour direct contact
with tumour site [9]. Keeping in these, the dynamics of tumour
cells represented by following differential equation.
used for the high cancer clearance
during gene therapy with the effector cells negative response.
The single-dose radiation γ kills only the tumour direct contact
with tumour site [9]. Keeping in these, the dynamics of tumour
cells represented by following differential equation.
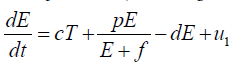
The overall model: With the above discussion, we may finalize
our model, which is 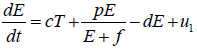
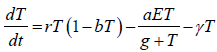
Assumptions:
1. The effector cells E(t) proliferate by itself with a decreasing function of Michaelis-Menten form
2. The effector cells E(t) arise with direct contact of tumour T(t) Both the two therapies can have the ability to clear the tumour at the same time at a different level
3. Gene therapy clears the tumour combined with effector cells E(t)
4. Radiation γ supply directly to the tumour site such that it kills tumour cells T(t) only
Parameters
Positivity and bounded-ness
Since the right-hand side of the system (3) is completely continuous and locally Lipschitzian on C, the solution (E(t), T(t)) of the model with initial conditions E(0) ≥ 0, T(0) ≥ 0 exists and is unique on (ζ, 0), where 0 < ζ ≤ ±∞ [18]. From system with initial conditions E(0) ≥ 0, T(0) ≥ 0, we have from the second equation of the system.
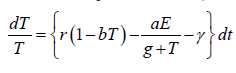
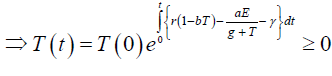
Again
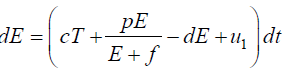
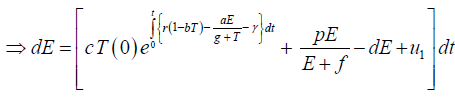
Since,
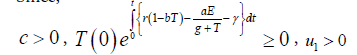
Therefore, we can drop these non-negative quantities, hence we get
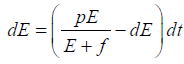
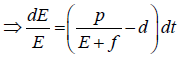
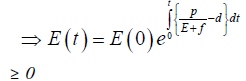
Hence, all the solution of the system with initial conditions E(0) ≥ 0 and T(0) ≥ 0 exists in the interval (0,1) and E (t) ≥ 0 and T(t) ≥ 0 for all t ≥ 0
From the second equation of system, it follows that
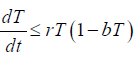
From the standard Kamke comparison theory [19], we get
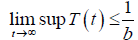
Now, from the first equation of the system (3), it follows that
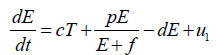
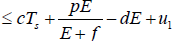
[Since T (t) bounded, Let sup T(t)=Ts
Taking, cTs + u1=K
[By assumption and parameter values this is constant]
Hence,
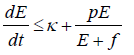
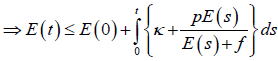
The generalised Gronwall Lemma [20] gives E (t)<M1 where M1 is uniformly bounded.
Therefore, T (t) of the system subject to initial conditions E (0) ≥ 0, T (0) ≥ 0 is bounded but E (t) may be bounded under some conditions among parameters and the bound of T (t) for t>0.
Local stability analysis at equilibrium points
In this section, we will study the existence and stability analysis of the system (3) at various equilibrium points. The equilibrium points of the system (3) are
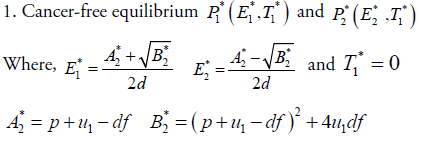
2. Cancer infected equilibrium 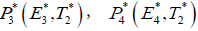
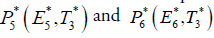
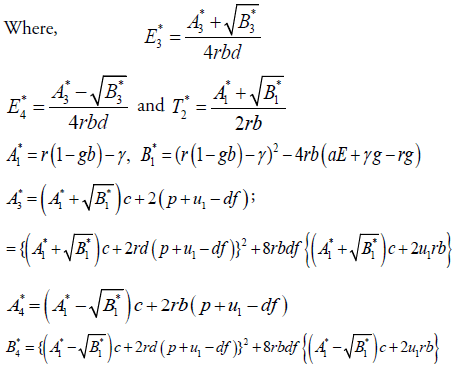
For stability analysis linearizing the system (3) to obtain Jacobian as follows:
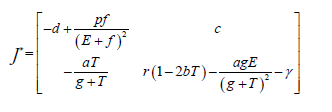
Local stability at each equilibrium point is checked by using Lemma 2.1 and the parameter Table 1 and has the following results.
The coexistence of both effector and tumour cell: With using
the value of the parameters from Table 1 and the radiation dose γ=0.1 the systems has two biologically feasible equilibrium
points out of which 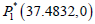 are cancer-free shows saddle
point behaviour with the unstable result and cancer infected
equilibrium point
are cancer-free shows saddle
point behaviour with the unstable result and cancer infected
equilibrium point 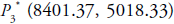 shows inward spiral
behaviour with locally asymptotically stable nature. Hence,
at this point, both effector and tumour compete with each
other in presence of radiogenic therapy. That means both cells
population goes to damped oscillation behaviour about zero
instead of asymptotes to zero (Figure 1a).
shows inward spiral
behaviour with locally asymptotically stable nature. Hence,
at this point, both effector and tumour compete with each
other in presence of radiogenic therapy. That means both cells
population goes to damped oscillation behaviour about zero
instead of asymptotes to zero (Figure 1a).
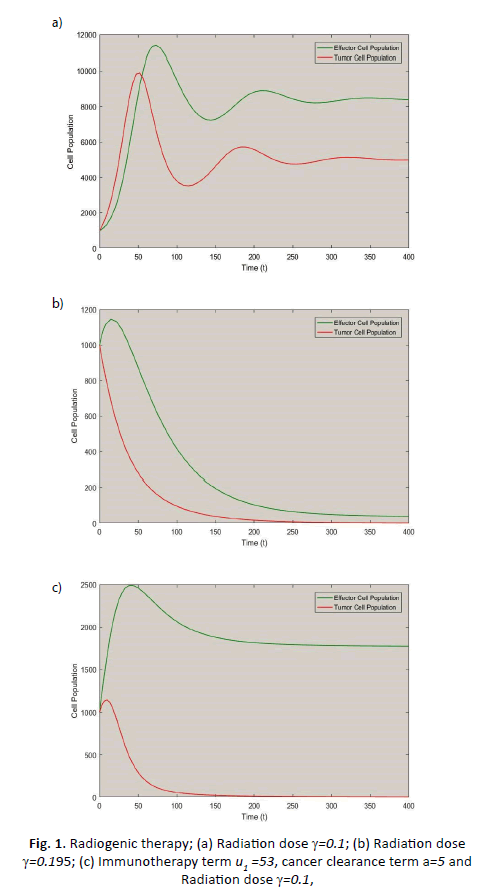
Figure 1: Radiogenic therapy; (a) Radiation dose γ=0.1; (b) Radiation dose γ=0.195; (c) Immunotherapy term u1 =53, cancer clearance term a=5 and Radiation dose γ=0.1,
The radiogenic therapy may cut out: Employing the values
presented in Table 1 as well as radiation dose γ=0.195 number of stationary points is only one 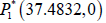 which
is cancer-free. This stationary point is asymptotically stable
and the system shows nodal sink nature at this equilibrium.
That means the effector cell population incorporates with the
treatment given can suppress the tumour growth to zero with
time increase (see Figure 1b). However, because of the higher
dose of radiation, which gives a negative impact on effector
cells, the effector cell population also goes down rapidly with
the increase of time. Which is not the aim of the treatment and
the treatment fails in this case.
which
is cancer-free. This stationary point is asymptotically stable
and the system shows nodal sink nature at this equilibrium.
That means the effector cell population incorporates with the
treatment given can suppress the tumour growth to zero with
time increase (see Figure 1b). However, because of the higher
dose of radiation, which gives a negative impact on effector
cells, the effector cell population also goes down rapidly with
the increase of time. Which is not the aim of the treatment and
the treatment fails in this case.
| Parameters | Meaning | Values | interval | Source |
|---|---|---|---|---|
| c | cancer antigenicity | 0.05 (1/time) | [10-3,0.5] | [12] |
| u1 | Immunotherapy term | 1 (cell/time) | [10-2,102] | [12] |
| p | proliferation rate of E | 0.1245 (1/time) | 0.1245 | [12] |
| f | half-saturation for E proliferation term | 10-3, (cells) | [10-5,1] | [12] |
| d | The half-life of effector cells E | 0.03 (1/time) | 0.03 | [12] |
| R | cancer growth rate | 0.18 (1/time) | [10-1,2] | [12] |
| b | cancer cell capacity | 10-9(1/cells) | 10-9 | [12] |
| a | cancer clearance term | 1 (1/cells) | [10-2,102] | [12] |
| g | Half-saturation, for cancer clearance | 105 (cells) | 105 | [12] |
Table 1. The parameter value for the model
The radiogenic therapy succeeds: Through the values presented
in Table 1 as well as the immuno-therapy dose u1 =53, cancer
clearance term a=5 and the radiation dose γ=0.1, there exists
only one equilibrium point 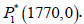 . That means, at this, the
body may be in a healthy stage as because the system behaves
asymptotically stable with nodal sink nature. The tumour cells
asymptote to zero rather than oscillating about zero (Figure 1c)
i.e., after a sufficient amount of time and a suitable amount
of radiation and immuno-therapy dose the tumour cells are
vanished by the use of treatment. This shows the combined
effect of radiogenic therapy.
. That means, at this, the
body may be in a healthy stage as because the system behaves
asymptotically stable with nodal sink nature. The tumour cells
asymptote to zero rather than oscillating about zero (Figure 1c)
i.e., after a sufficient amount of time and a suitable amount
of radiation and immuno-therapy dose the tumour cells are
vanished by the use of treatment. This shows the combined
effect of radiogenic therapy.
The initial values used in these simulations are E(0)=T(0)=1000.
Global Stability
Linear stability analysis shows how a system behaves in a
neighbourhood of an equilibrium point. It does not, however,
describe anything about what happens further away from
equilibrium. In this section, we will show the point 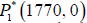 is globally stable by constructing a Lyapunov function, which
described the total eradication of the tumour.
is globally stable by constructing a Lyapunov function, which
described the total eradication of the tumour.
Define a Lyapunov functional of the model as
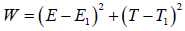
Differentiating on both sides with respect to time, we get
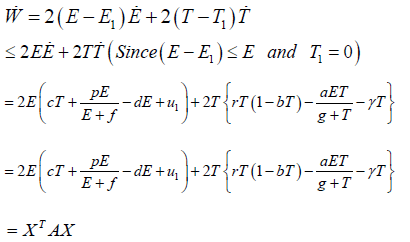
Where
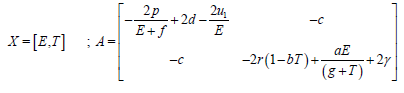
Here,
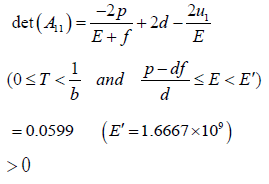
And
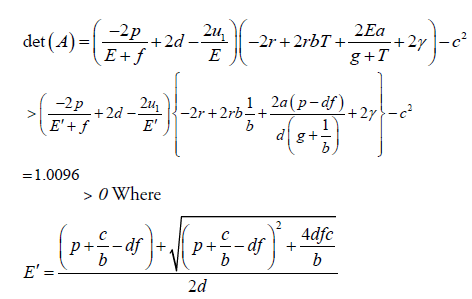
∴W <0, because the matrix A is positive definite.
The equilibrium point 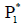 satisfies all the conditions of
Lyapunov stability theorem i.e. tumour-free equilibrium point
satisfies all the conditions of
Lyapunov stability theorem i.e. tumour-free equilibrium point 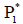 to be globally asymptotically stable [Lemma 2.3]. Hence,
the equilibrium point
to be globally asymptotically stable [Lemma 2.3]. Hence,
the equilibrium point 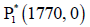 is globally asymptotically
stable on the domain
is globally asymptotically
stable on the domain 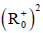 (where
(where 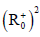 is denote the nonnegative
octant of R2) if the Lyapunov W<0 at this point
(Figures 2 and 3).
is denote the nonnegative
octant of R2) if the Lyapunov W<0 at this point
(Figures 2 and 3).
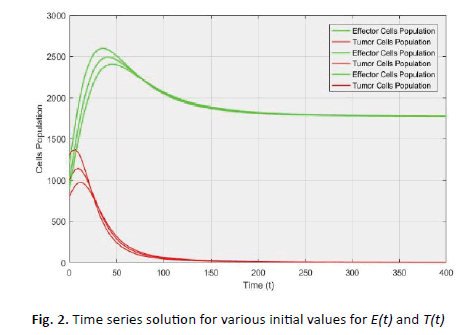
Figure 2: Time series solution for various initial values for E(t) and T(t)
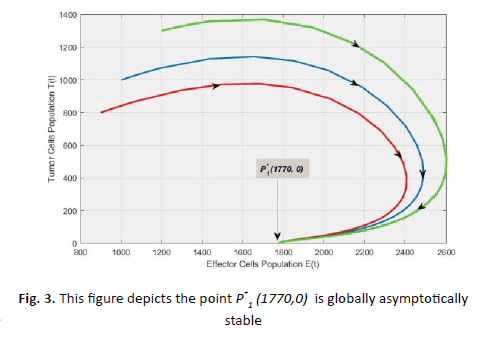
Figure 3: This figure depicts the point P*1 (1770,0) is globally asymptotically stable
Conclusion
Cancer research has undergone radical changes in the last
few decades. The main subject of this paper to investigate the
effectiveness of radiogenic therapy. Here, we have observed
that if we treat tumour site with sufficient amount of immunotherapy
drugs and radiotherapy dose under some circumstances,
cancer may be eradicated from the body. We further investigated
for the total eradication of cancer by checking global stability at
tumour free equilibrium. From our observation, the trajectory
of the system goes towards the point 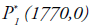 for various initial conditions (Figure 2) which described the global stability
of the system (Figure 3). Hence, we may conclude that cancer
may eradicate from the body with the use of radiogenic therapy
by choosing a suitable amount of drug dose. This research gives
small amounts of help to the oncologists in practice the cancer
treatment. In future, we will analyse the model with pulsed
radiation and optimal continuous radiation therapy using delay
differential equation for a better realistic scenario.
for various initial conditions (Figure 2) which described the global stability
of the system (Figure 3). Hence, we may conclude that cancer
may eradicate from the body with the use of radiogenic therapy
by choosing a suitable amount of drug dose. This research gives
small amounts of help to the oncologists in practice the cancer
treatment. In future, we will analyse the model with pulsed
radiation and optimal continuous radiation therapy using delay
differential equation for a better realistic scenario.
References
- Hashmi MU, Suleman M, Zaidi SMJ, Habib M. Modeling the tumor-immune interaction cultured with chemotherapy and cytokine interleukin il-2 under the influence of immunodeficiency viruses. Am Eurasian J Toxicol Sci. 2014;6:74-82.
- Latha N, Komahan G. Mathematical model of p53 gene in gene therapy treatment for lung cancer. IntJ Sci Res Develop. 2017;10:267-270.
- Dehingia K, Nath KC, Sarmah HK. Mathematical modelling of tumour-immune dynamics and cure therapy: a review of literature. J Nat Remedies. 2020;21:26-41.
- Robson T, Worthington J, McKeown SR, Hirst DG. Radiogenic therapy: novel approaches for enhancing tumor radiosensitivity. Technol Cancer Res Treat. 2005;4;343-361.
- Pappalardo F, Palladini A, Pennisi M. Mathematical and computational models in tumor immunology. Math Model Nat Phenom. 2012;7:186-203.
- Kirschner D, Panetta JC. Modeling immunotherapy of the tumor-immune interaction. J Math Biol. 1998;37:235-252.
- De Pillis LG, Radunskaya AE. A mathematical model of immune response to tumor invasion", computational fluid and solid mechanics 2003, Proceedings of the Second M.I.T. Conference on Computational Fluid Dynamics and Solid Mechanics. 2003;1661-1668.
- De Vita V, Hellman S, Rosenberg S. Cancer: principles and practice of oncology. Lippincott Wiliams and Wilkins, 7th edition, 2000.
- Isea R, Lonngren KE. A mathematical model of cancer under radiotherapy. Intern J Pub Health Res. 2015;3:340-344.
- Maurici D, Hainaut P. TP53 gene and p53 protein as targets in cancer management and therapy. Biotechnol. 2001;12:1-15.
- Teh BS, Aguilar-Cordova E, Vlachaki MT. Combining radiotherapy with gene therapy (from the bench to the bedside): a novel treatment strategy for prostate cancer. The Oncologist. 2002;7:458-466.
- Tsygvintsev A, Marino S, Kirschner DE. A mathematical model of gene therapy for the treatment of cancer, Springer-Verlag, Berlin-Heidelberg- New York. 2013;10:355-373.
- Amer MH. Gene therapy for cancer: present status and future perspective. Mol Cell Ther. 2014;2:27.
- Blair RH, Trichler DL, Gaille DP. 2012. Mathematical and statistical modelling in cancer system biology. Front Physiol. 2012;3:1-8.
- Mamat SM, Kartono A. Mathematical model of cancer treatment using immunotherapy, chemotherapy and biochemotherapy. App Math Sci. 2013;7:247-261.
- Roose T, Champman SJ, Maini PK. Mathematical models of avascular tumour growth. Siam Rev. 2007;49:179-208.
- Roussel MR. Stability analysis for ODEs. Nonlinear dynamics, lecture notes. University Hall, Canada. 2005.
- Sharma S, Samanta GP. Dynamical behavior of a tumor-immune system with chemotherapy and optimal control. J Nonlinear Dynam. 2013;2013:1-13.
- Pinho ST, Bacelar FS, Andrade S, Freedman HI. A mathematical model for the effect of anti-angiogenic therapy in the treatment of cancer tumors by chemotherapy. Nonlinear Anal RealWorld Appli. 2013;14:815-828.
- Rihan FA, Abdelrahman DH, Al-Maskari F. Delay differential model for tumour-immune response with chemoimmunotherapy and optimal control.Comput Math Method M. 2014;2014:1-15